Definition of Fuzzy
Set
When
a collection of things belong to a certain definition, it is known as a Set.
When these set show a degree of membership, it is known as fuzzy set.
Fuzzy set theory was given by the Professor Lofti Zadeh and Dieter Klaua, University
of California 1965.
When
we use classical set theory, the memberships of element are represented in the
Binary terms. In Binary terms, identifying
whether an element belongs to a set or does not is known as bivalent condition.
But in fuzzy set, we can gradually assess the membership of element of a set.
In Fuzzy Set, the classical set is generalized, as the indicator
functions of the classical set are special case membership functions of fuzzy
set. These binary sets are usually called crisp sets in case of fuzzy set. In
general, we are just trying to analyse or arrive at a conclusion whether a
given observation lies within the set or outside or as a continuum as a partial
member of the set.
Why Fuzzy Set is used?
We
use the fuzzy set when we have incomplete information on a particular
case. The fuzzy set is more often used in
Bio informatics as many of the information in this stream are random or
uncertain. In these cases, fuzzy set theory provides a sound tool to ascertain
the answer of the bio informatics problems.
How Fuzzy Set is used?
In
fuzzy set, lets say ‘A’ is the membership function; its range will be within
unit interval. At any point the value of function will be the degree of
membership of the point in set A.
We
have set of car for sale in the area.
A
= Fuzzy Set of car to be purchased
Value
assigned for each car will be in between 0 to 1 which will be the degree of
membership of the particular car in the Fuzzy set A.
Therefore, the Fuzzy membership function will measure, the
attractiveness for the particular car. Like in this case, you like a car very
much, its value u will be in larger side say 0.8 or 0.9 but for the less
attractiveness of the car it will be on lower side say 0.2 or 0.10.
X1, . . . , Xn be iid normal (µ, σ2).
X¯ = Pn i=1 Xi/n and S 2 = Pn
i=1(Xi − X¯) 2/ (n − 1) then
(X¯ − tn, 0.025S/√ n, X¯ + tn,
0.025S/√ n)
It is a 95% confidence interval for
µ.
Therefore, function of µ it has
constant coverage of the probability.
Example of Fuzzy Set
We
make a set of tall men and make an assumption that people above 6 feet will be
tall and represent the same as a set. Now the populations that we will consider
will be either present in the set or absent in the set. These membership
functions work better in the binary function, however in the real-world
function, they do not hold well. In the real-world operation, it will put a
person with height of 6’1inch and 7’2 inch in the same set and similarly it
will put → 5’11 and 6’0 in different set though they have only just 1 inch of
difference. It means that this kind of set will put it as tall and not
tall. Therefore, that will imply à 5’11 is not tall in the set and 6’0 inch is
tall in this set.
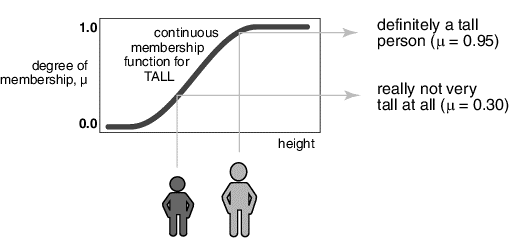
In fuzzy Set, the representation for taller people will be in much better way. Below is the diagram for the representation of taller people made by the fuzzy set.
The
membership function gives value of fuzzy set underneath the horizontal axis.
The vertical axis, provide membership value of
the height in the fuzzy Set. In the given example, one person has a mean
average height of 0.30 therefore it is short heighted while other person has a
mean average height of 0.90 therefore it is in the long heighted category. Here
the entire membership element lies below the line. What is Crisp Set? A
crisp set is a classical set where member can either be in the set or
outside the set while in the fuzzy set member can be partially in the set. For
Crisp set, the value is assigned either 0 or 1 since it follows the binary
system for each element of the universe. The assignment of the Binary number
differentiates the crisp set as member and the non- member. The
crisp set is also known as the classical set or ordinary set theory.
Therefore, it’s a conventional set for which elements are either members or
non- members. What is membership function in Fuzzy Logic? The membership function is a
curve to define each element in the input space; it is valued as degree of
membership between 0 to 1. The input space is also known as ‘Universe of
Discourse’. The only condition for the
membership function is to lie between 0 to 1. We can express a classical set as
follows: A = {x | x >
6} The fuzzy set is the extension of
the classical set. Let X= Input space or Universe of Discourse Then fuzzy set A for X will be as
follows: µA(x) = memberships
function of x in A In fuzzy set, each element of X will
have membership value in between 0 to 1. Fuzzy Logic It
is a many valued logic where the true value of the logic lies between the real
number 0 to 1. The fuzzy logic is used in case of the partial truth, where the
true value lies in between truth and completely false value. We
can apply fuzzy logic for sub range of continuous variables. For example, if temperature
of anti–lock brakes has separate membership function, where we need a
particular temperature range to control the Brake properly, then the function
will map the value between 0 to 1 ranges for the temperature. These truth
values is used to determine the temperature controlled method for Brake. The cold, warm and the hot are various
temperatures represented in the functional mapping scale. Fuzzy Set Theory and its Application The
fuzzy set theory is used in the cases where the data cannot be gathered with
certainty and reasonableness. Fuzzy
logic for the very first time was successfully used and implemented in Japan to
improve the economy, comfort and precision while travelling in a high- speed
train. Fuzzy
Set Approach in Data Mining: In
the recent years, the fuzzy set theory was used to explore several aspects of
data mining and other knowledge discovery method. As many of the data in the
data mining are vague therefore fuzzy set helps in providing value to each
element. Fuzzy
Set Application in Social Science: The
Fuzzy set theory is also used in the social science. The main aim of using
fuzzy set in this case is that we do not have any precise data on any research
topic. We can use fuzzy set for the measurement. Fuzzy
Set Application in Medical Science: Similarly,
we can use fuzzy set in case of medical science also; to get the conclusion
from the subjective data; we can provide elementary value for the conclusion
result. Other
areas of application of fuzzy technology are in the fields of artificial
intelligence, computer science, decision making, management science, operations
research, robotics and many others. Therefore, in case of crisp set we will have functions only as 1 or 0;
it can be either within the set or out of the set like tall or dwarf. In case
of Fuzzy set the data are in between u=0 and u=1. It can have any value in
between and the value represent more characteristics as 0.8 will tell the
taller men while 0.2 will tell the dwarf men. The advantage is that middle
values too can be utilized in case of fuzzy set as compared to crisp set. When
we have to derive any conclusion from the data which are not certain then we
can use the Fuzzy Theory. The Fuzzy set has been used in the wide variety of
ranges like medical sciences data or the social science data analysis or in
case of data mining to conclude the result where we do not have the precise
data. The
fuzzy set also generalizes the classical set since the indicator functions of
classical set are but only the special membership cases of the fuzzy sets. In general,
in case of incomplete and uncertain information, we give preference to the
fuzzy set instead of the classical crisp set. In
general, fuzzy set has following set namely, (U, m), where u represents the
set, while m: u - [0, 1] The
fuzzy set defines the set of membership as Possibility distribution. In case of
fuzzy set, we can use n possible sets of events and use to generate a single
possible outcome. It can allow its members to have different grades of
memberships. In context of fuzzy logic, we can conclude the following points: The
use of fuzzy set can be seen as the paradigm shift in
the statics process, we can conclude that the use of fuzzy set in the light of
fuzzy logic has made the data mining easy for the researchers. Its utilization
has increased from the data mining to medical science and social science.








 USA
USA  India
India