Sample Mean Assignment Help | Statistics Homework Help | Just Question Answer

What is Sample?

A finite subset of statistical individuals in a population is called a sample and the number of individuals in a sample is called sample size.

Example

In a shop we assess the quality of sugar, wheat or any other commodity by taking a handful of it from the bag and then decide to purchase it or not. On examining the sample of a particular stuff we arrive at a decision of purchasing or rejecting that stuff. The error involved in such approximation is known as sampling error.

Population

In a statistical investigation the interest usually lies in the assessment of the general magnitude and the study of variation with respect to one or more characteristics relating to individuals belonging to a group. This group of individuals under study is called population.

Example

If we want to have an idea of the average per capita income of the people in Canada, we will have to enumerate all the earning individuals in the country, which is rather a very difficult task.

Sampling Distribution

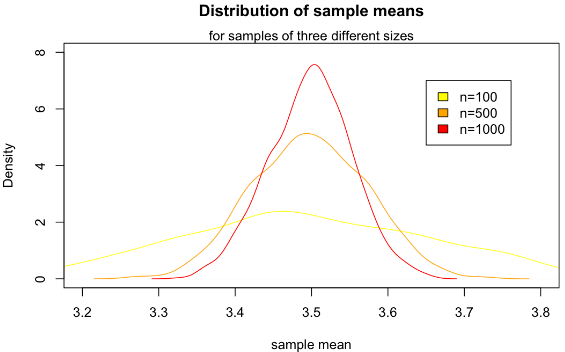
The number of possible samples of size n that can be drawn from a finite population of size N is ^NC_n. if N is large or infinite then we can draw a large number of such samples. For each of these samples we can compute a statistics, say ‘t’….., e.g. mean, variance, etc., which will obviously vary from sample to sample. The aggregate of the various values of the statistics under consideration so obtained may be grouped into a frequency distribution which is known as the sampling distribution of the statistics. Thus we can have the sampling distribution of the sample mean and sample variance etc.

Mean of the Sample Mean:

There is simple relationship between the mean of the variable and the mean of the variable under consideration: They are equal or in other words for any particular sample size, the mean of all possible sample means equal the population mean. The equality holds regardless of the size of the sample.

”For samples of size k, the mean of the variable equals the mean of the variable under consideration. In symbols,”

Standard Deviation of the Sample Mean

For samples of size k, the standard deviation of the variable equals the standard deviation of the variable under consideration divided by the square root of the sample size. In symbols,

Example

The mean living space for single family detached homes is 1742 sq. ft. Assume a standard deviation of 568 sq. ft. For sample of 25 single family detached homes, determine the mean and standard deviation of the sample mean.

Solution: Using equation (i) and (ii)

We have,

Mean = 1742 sq. ft.

Standard deviation = 568/5 = 113.6

Hence, for a sample of 25, the mean and standard deviation of the sample mean is 1742 sq. ft. and 113.6 sq. ft. respectively.

Sampling Distribution of Sample Mean

Suppose that a variable y of a population has mean µ and standard deviation σ. Then, for sample of size k,

• Estimating Population Meanð σ is known

  Assumptions:

  1. The sample is simple random sample (equal chances of being selected).
  2. The value of the population standard deviation is known.
  3. Either or both of these conditions are satisfied: The population is normally distributed or k > 30.
  In the above assumptions, we see that we want to estimate an unknown population mean µ, but we must know the value of the population standard deviation σ. It would be unusual set of circumstances that allow us to know σ without knowing µ. After all, the only way to find the value of σ is to compute it from all of the known population values, so the computation of µ would also be possible and, if we can find the true value of µ, there is no need to estimate it.
  
• 
  
• 
  
• 
  

• Estimating Population Mean σ is Unknown

  Assumptions

  • The sample is a simple random sample.
  • Either a sample is from a normally distributed population or k > 30
  We can usually consider the population to be normally distributed after using the sample data to confirm that there are no outliers and a histogram has a shape that is not very far from a normal distribution. The sampling distribution of sample mean is exactly a normal distribution with mean and standard deviation
•