1. What is Standard Deviation?
The
quantitative degree by which every value in a given data varies from a Measure
of Central Tendency is known as Standard Deviation (S.D.) It is denoted by
Greek small letter σ. It is the positive square root of the Arithmetic mean of
squares of deviations of a given data set from their Arithmetic mean.
The term ‘Standard Deviation’ was first used by Karl Pearson in 1894.
Question:
What is Measure of Central Tendency?
Answer:
A single value which defines the
properties of a given distribution is known as Measure of Central Tendency.
Mean, mode and median are three main Measure of Central Tendency. Mean
is the most frequently used Measure of Central Tendency.
Why is mean used as a Measure of
Central Tendency?
Answer:
Mean is the sum of all the values of
an observation divided by the total number of observations in a given data.
Formula of Arithmetic
Mean
For the Frequency Distribution
Arithmetic Mean is used as a Measure of Central Tendency quite frequently
because of the following merits:-
- It covers all the values of an observation.
- It allows further mathematical treatment.
- The error is minimized by using Arithmetic Mean for
every value.
- Mean is the only value for which the sum of deviations
for an observation is zero.
In case of Standard Deviation, Mean
is represented by x-bar and in case of population observations mean is denoted
as Greek letter mu (µ). Unlike Standard Deviation, the formula of mean
remains the same in both the cases.
2. Formula for Standard Deviation
Population Standard
Deviation
Sample Standard
Deviation
Question:
Why are there two different
methods of Standard Deviation S.D.?
Answer:
S
is an unbiased estimator for Population Standard Deviation. However, Sigma
(σ) is a biased estimator for Population S.D. For large samples, the bias
starts tending to zero as n increases. Hence, sigma is also considered as an
equally important S.D.
For
understanding the concept of Standard Deviation, the understanding of Variance
is important
Question:
What is Variance?
Answer:
Given
a data set, the values vary about a measure of central tendency (mean, median,
mode etc) and these measures are known as measures of variation or dispersion.
Variance is one of the frequently used measures of dispersion where,
For Discrete Data:

Finding Standard Deviation through
Variance:
For finding Standard Deviation in case of ungrouped data (Discrete Data) or grouped data (Continuous Data) one can use, methods (1) and (2) given above respectively.
|
S.D.
= √Variance |
3. How to Find Out Standard Deviation
In case of Population Values,
procedural steps to find out Standard Deviation are as follows:
Step 1: Find µ.
Step 2: For each value, subtract the mean from the value and square
it.
Step 3: Add all the values obtained through step 1.
Step 4: Divide the values obtained through 3 by total number
of observations. (N in case of grouped data and ∑ frequencies in case of
ungrouped data). We obtain the variance after this.
4. Example of Standard Deviation
Question:
For Discrete Data, consider marks
obtained in a class of 10 students (out of 50): 10, 20, 45, 45, 24, 8, 19, 45,
23, 35.
Solution:
Here,
N = 10
The mean of the given Data set is (10 + 20 + 45 + 45 + 24 + 8 + 19 + 45 + 23 +
35)/10 = 27.4
|
Xi
(Observations) |
(xi
- µ) |
(xi
- µ)2 |
|
10 |
-17.4 |
302.76 |
|
20 |
-7.4 |
54.76 |
|
45 |
17.6 |
309.76 |
|
45 |
17.6 |
309.76 |
|
24 |
-3.4 |
11.56 |
|
8 |
-19.4 |
376.36 |
|
19 |
-8.4 |
70.56 |
|
45 |
17.6 |
309.76 |
|
23 |
-4.4 |
19.36 |
|
35 |
7.6 |
57.76 |
|
1.N
= 10 |
2.∑(xi
- µ) = 0 |
3.∑(xi
- µ)2 = 1822.4 |
Here, N=10, variance= (3/N) = 182.4
S.D. = √variance → Standard
Deviation = 13.49963
Here, S.D. is very high which
indicates that there is a very high variation in marks of students in the
class.
Question:
Given no. of people belonging to different age groups. Find the S.D. for grouped data?
|
Age
group |
Mid-value |
Frequency |
d
= x - A/h |
fd |
fd2 |
|
20-30 |
25 |
3 |
-3 |
-9 |
27 |
|
30-40 |
35 |
61 |
-2 |
-122 |
244 |
|
40-50 |
45 |
132 |
-1 |
-132 |
132 |
|
50-60 |
55 |
153 |
0 |
0 |
0 |
|
60-70 |
65 |
140 |
1 |
140 |
140 |
|
70-80 |
75 |
51 |
2 |
102 |
204 |
|
80-90 |
85 |
2 |
3 |
6 |
18 |
|
Total |
|
542 |
|
-15 |
765 |
Solution:
Here, we take d = (x - 55)/10 now,
Mean = A + h* ∑fd/N where N= ∑f
Mean = 54.72 years.
{Variance is independent of change of origin but not of scale}
→ σ = 11.88 years
5. Relationship of Standard Deviation with other Statistical
Measures
Relationship between Standard
Deviation and Variance
- Standard Deviation is positive square root of Variance.
Relationship between Standard
Deviation and Precision
- Standard Deviation and precision are inversely related
to each other.
6. Implications of Standard Deviation
Degree of variability of given
observations. To understand it in a better way, consider three sets of
observations given below:
|
1. |
14 |
2 |
1 |
3 |
5 |
Mean = 5
Standard Deviation = 5.24404
Variance = 27.5
|
2. |
5 |
4 |
6 |
4 |
6 |
Mean = 5
Standard Deviation = 1
Variance = 1
|
3. |
5 |
5 |
5 |
5 |
5 |
Mean = 5
Standard Deviation = 0
Variance
= 0
In
these three observations, we noticed that the mean is 5 in all the three cases,
whereas the Standard Deviation in 3rd observation is 0 since there
is no variation in values. In second observation, the Standard Deviation is
very less since the values are closely related to each other and in first case,
the Standard Deviation is very high due to very high degree of variation in the
values.
7. Important Properties of Standard Deviation
- Standard Deviation is always positive.
- Standard Deviation of a constant is 0 i.e. σ (c)
= 0 where c is a constant.
- σ (X + c) = σ (X)
- σ (c * X) = |c|* σ (X)
- The above two properties show that Standard Deviation
is independent of change of origin but not of change of scale.
- σ (X + Y) = √(variance(X) + variance(Y) +
2*covariance(X * Y)
- Standard Deviation is high when difference between
values is large.
- Standard Deviation is nothing but sum of distance of
values from mean divided by total number of observations.
8. Standard Deviation and Standard Normal Distribution
Figure
of normal distribution with mean
µ
If
X is a random variable which is distributed normally such that X~N (µ, σ2)
which has mean µ and σ S.D. then, the length within 2σ limits covers 68.26 of
the area of the distribution. The area within 4 σ limits i.e. from µ - 2*σ to µ
+ 2*σ covers 95.46 area (% probability), the area between µ-3 *σ and µ+3 *σ is
99.7773 and rest of the area falls after µ±3σ.
9. Real Life Examples where Standard Deviation is used
- In finance, Standard Deviation
is applied to the annual rate of return of an investment to
measure the investments volatility.
- Standard Deviation is used in
models based on real life to check the variation in policies in real life
situation in a much easier way.
- Standard Deviation is used to
check hypothesis testing.
- Standard Deviation is used to
find out confidence limits which is used to find out if there is a
significant deviation in quality of the products and the limit within
which defects are permissible/tolerable limits and limits after which
measures are to be taken.
- Standard Deviation is used to
find correlation coefficient between two random variables.
- Standard Deviation is widely
used in Normal Distribution.
- Standard Deviation is used to check p-values, t-test.
Question:
How to calculate Standard Deviation
using excel or Scientific Calculators?
Solution:
Excel and Scientific Calculators
both have an option to calculate the population as well as the sample S.D.
Calculating of S.D. Using Excel
The command to find S.D. in excel is
STDEVP (values) where values are chosen from a column.
Calculating of S.D. Using Casio
Calcuator Fx 115-Es
- Click on the mode button.
- Press 3 for Stats.
- 1- for S.D. of single variable.
- Enter your data
- AC
- Shift +1 for Stats
- Select σx option.
10. Precaution that should be taken while using Standard
Deviation


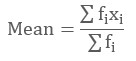
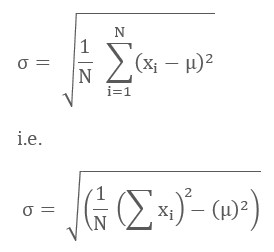
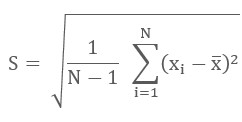








 USA
USA  India
India